Что такое метод канонического разложения данных акселерограмм

Случайная величина Vназываетсяцентрированной , если ее математическое ожидание равно 0. Элементарным центрированным случайным процессом называется произведение центрированной случайной величиныVна неслучайную функцию φ(t):X(t)=Vφ(t). Элементарный центрированный случайный процесс имеет следующие характеристики:

Выражение вида
, где φ k ( t ), k =1;2;…-неслучайные функции; , k =1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X ( t ), при этом случайные величины называются коэффициентами канонического разложения; а неслучайные функции φ k ( t ) - координатными функциями канонического разложения.

Рассмотрим характеристики случайного процесса

Так как по условию
то

Очевидно, что один и тот же случайный процесс имеет различные виды канонического разложения в зависимости от выбора координатных функций. Более того, даже при состоявшемся выборе координатных функций существует произвол в распределении случайных величин V к. На практике по итогам экспериментов получают оценки для математического ожидания и корреляционной функции:
. После разложения
в двойной ряд Фурье по координатным функциям φ к (t):

получают значения дисперсий
случайных величинV k .

4.2. Понятие обобщенной функции. Дельта-функция Дирака. Интегральное каноническое представление случайных процессов.

Обобщенной функцией называется предел последовательности однопараметрического семейства непрерывных функций.

Дельта-функция Дирака
- это обобщенная функция, являющаяся результатом предельного перехода при
в семействе функций

Среди свойств -функции отметим следующее:

2.

3. Если f(t)- непрерывная функция, то

Случайный процесс Х( t ), корреляционная функция которого имеет вид называется нестационарным «белым шумом». Если W ( t 1 )= W - const , то Х( t )-стационарный «белый шум».

Как следует из определения, никакие два, даже сколь угодные близкие, сечения «белого шума» не коррелированны. Выражение W(t) называетсяинтенсивностью «белого шума».

Интегральным каноническим представлением случайного процесса Х( t ) называется выражение вида
где
- случайная центрированная функция;
- неслучайная функция непрерывных аргументов

Корреляционная функция такого случайного процесса имеет вид:

Можно показать, что существует неслучайная функция G(λ) такая, что

где G(λ 1) - плотность дисперсии; δ(х) - дельта-функция Дирака. Получаем

Следовательно, дисперсия случайного процесса Х(t):

.

4.3. Линейные и нелинейные преобразования случайных процессов

Рассматривается следующая задача: на вход системы (устройства, преобразователя) Sподается «входной сигнал», имеющий характер случайного процесса Х(t). Система преобразовывает его в «выходной сигнал»Y(t):

.

Формально преобразование случайного процесса Х(t) вY(t) может быть описано с помощью так называемого оператора системы А t:

Y(t)=A t (Х(t)).

Индекс tпоказывает, что данный оператор осуществляет преобразование по времени. Возможны следующие постановки задачи о преобразовании случайного процесса.

Известны законы распределения или общие характеристики случайного процесса Х(t) на входе в системуS, задан оператор А t системыS, требуется определить закон распределения или общие характеристики случайного процессаY(t) на выходе системыS.

Известны законы распределения (общие характеристики) случайного процесса Х(t) и требования к случайному процессуY(t); надо определить вид оператора А t системыS, наилучшим образом удовлетворяющего заданным требованиям кY(t).

Известны законы распределения (общие характеристики) случайного процесса Y(t) и задан оператор А t системыS; требуется определить законы распределения или общие характеристики случайного процесса Х(t).

Принята следующая классификация операторов А t системыS:

Операторы системы

Линейные LНелинейныеN

Линейные однородные L 0 Линейные неоднородныеL н

Рассмотрим воздействие линейной неоднородной системы

L н (...)=L 0 (…)+φ(t)

на случайный процесс Х(t), имеющий следующее каноническое разложение:

.

Получаем:

введем обозначения

тогда каноническое разложение Y(t) приобретает вид:

.

Математическое ожидание случайного процессаY(t):

корреляционная функция случайного процесса Y(t):

следовательно,

С другой стороны

Дисперсия случайного процесса Y(t):

В заключении этого пункта отметим, что операторы дифференцирования и интегрирования случайных процессов являются линейными однородными.

2. Рассматривается квадратичное преобразование:

Y(t)=(X(t)) 2 ,

V k -центрированные случайные величины, имеющие симметричное относительно нуля распределение; любые четыре из них независимы в совокупности. Тогда

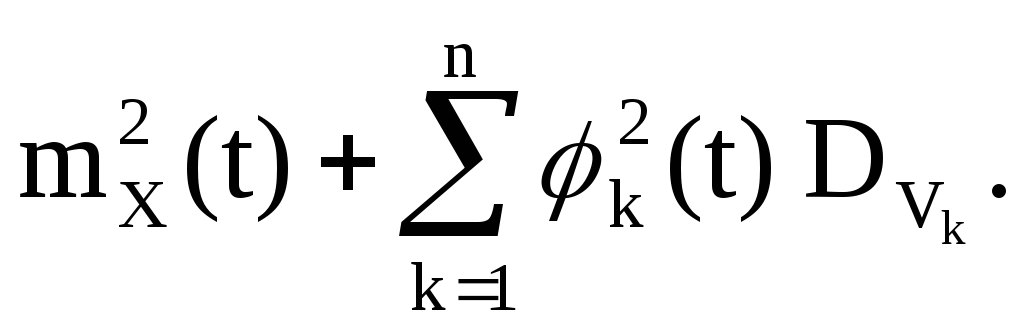
Введем неслучайные функции

и случайные величины

тогда случайный процесс Y(t) приобретает вид

Получено каноническое разложение случайного процесса Y(t). Корреляционная функцияY(t):

В подразделе 15.7 мы познакомились с общими правилами линейных преобразований случайных функций. Эти правила сводятся к тому, что при линейном преобразовании случайной функции ее математическое ожидание подвергается тому же линейному преобразованию, а корреляционная функция подвергается этому преобразованию дважды: по одному и другому аргументу.

Правило преобразования математического ожидания очень просто и при практическом применении затруднений не вызывает. Что касается двойного преобразования корреляционной функции, то оно в ряде случаев приводит к чрезвычайно сложным и громоздким операциям, что затрудняет практическое применение изложенных общих методов.

Действительно, рассмотрим, например, простейший интегральный оператор:

Согласно общему правилу корреляционная функция преобразуется тем же оператором дважды:

Очень часто бывает, что полученная из опыта корреляционная функция K x (t, t") не имеет аналитического выражения и задана таблично; тогда интеграл (16.1.2) приходится вычислять численно, определяя его как функцию обоих пределов. Это - задача очень громоздкая и трудоемкая. Если даже аппроксимировать подынтегральную функцию каким-либо аналитическим выражением, то и в этом случае чаще всего интеграл (16.1.2) через известные функции не выражается. Так обстоит дело даже при простейшей форме оператора преобразования. Если же, как часто бывает, работа динамической системы описывается дифференциальными уравнениями, решение которых не выражается в явной форме, задача об определении корреляционной функции на выходе еще более осложняется: она требует интегрирования дифференциальных уравнений с частными производными.

Рис. 16.1.1

В связи с этим на практике применение изложенных общих методов линейных преобразований случайных функций, как правило, оказывается слишком сложным и себя не оправдывает. При решении практических задач значительно чаще применяются другие методы, приводящие к более простым преобразованиям. Один из них - так называемый метод канонических разложений, разработанный В. С. Пугачевым, и составляет содержание данной главы.

Идея метода канонических разложений состоит в том, что случайная функция, над которой нужно произвести те или иные преобразования, предварительно представляется в виде суммы так называемых элементарных случайных функций.

Элементарной случайной функцией называется функция вида:

где К - обьиная случайная величина;

Элементарная случайная функция является наиболее простым типом случайной функции. Действительно, в выражении (16.1.3) случайным является только множитель V, стоящий перед функцией ф (/); сама же зависимость от времени случайной не является.

Все возможные реализации элементарной случайной функции X(t) могут быть получены из графика функции х = ф (?) простым изменением масштаба по оси ординат (рис. 16.1.1). При этом ось абсцисс (х=0) также представляет собой одну из возможных реализаций случайной функции X(t ), осуществляющуюся, когда случайная величина V принимает значение 0 (если это значение принадлежит к числу возможных значений величины V).

В качестве примеров элементарных случайных функций приведем функцииX(t) =Fsin/(рис. 16.1.2) иX(t) =Vt 2 (рис. 16.1.3).

Элементарная случайная функция характерна тем, что в ней разделены две особенности случайной функции: случайность вся сосредоточена в коэффициенте V, а зависимость от времени - в обычной функции ф (/).

Рис. 16.1.2

Рис. 16.1.3

Определим характеристики элементарной случайной функции (16.1.3). Имеем:

где т„ - математическое ожидание случайной величины V.

Если m v = 0, математическое ожидание случайной функции X(t) также равно нулю, причем тождественно:

Мы знаем, что любую случайную функцию можно центрировать, т.е. привести к такому виду, когда ее математическое ожидание равно нулю. Поэтому в дальнейшем мы будем рассматривать только центрированные элементарные случайные функции, для которых m v = 0;

V = V; m x (t) = 0. Определим корреляционную функцию элементарной случайной функции X(t). Имеем:

где D - дисперсия величины V.

Над элементарными случайными функциями весьма просто выполняются все возможные линейные преобразования.

Например, продифференцируем случайную функцию (16.1.3). Случайная величина V , не зависящая от t, выйдет за знак производной, и мы получим:

Аналогично

Вообще, если элементарная случайная функция (16.1.3) преобразуется линейным оператором L, то при этом случайный множитель V, как не зависящий от /, выходит за знак оператора, а неслучайная функция ф (?) преобразуется тем же оператором L:

Значит, если элементарная случайная функция поступает на вход линейной системы, то задача ее преобразования сводится к простой задаче преобразования одной неслучайной функции ф (/). Отсюда возникает идея: если на вход динамической системы поступает некоторая случайная функция общего вида, то можно ее представить - точно или приближенно - в виде суммы элементарных случайных функций и только затем подвергать преобразованию. Такая идея разложения случайной функции на сумму элементарных случайных функций и лежит в основе метода канонических разложений.

Пусть имеется случайная функция:

Допустим, что нам удалось - точно или приближенно - представить ее в виде суммы

где V/ - случайные величины с математическими ожиданиями, равными нулю; ср,-(0 - неслучайные функции; m x (t) - математическое ожидание функции X(t).

Условимся называть представление случайной функции в форме (16.1.6) разложением случайной функции. Случайные величины К, V 2 , V m будем называть коэффициентами разложения, а неслучайные функции ф^/), ф 2 (/), , Ф, н (0 - координатными функциями.

Определим реакцию линейной системы с оператором L на случайную функцию X(t), заданную в виде разложения (16.1.6). Известно, что линейная система обладает так называемым свойством суперпозиции, состоящим в том, что реакция системы на сумму нескольких воздействий равна сумме реакций системы на каждое отдельное воздействие. Действительно, оператор системы L, будучи линейным, может по определению применяться к сумме почленно.

Обозначая Y(t) реакцию системы на случайное воздействие Х(1), имеем:

Придадим выражению (16.1.7) несколько иную форму. Учитывая общее правило линейного преобразования математического ожидания, убеждаемся, что L{m x {1)} = m y (t).

Обозначая

Выражение (16.1.8) представляет собой не что иное, какразложение случайной функции Y(t) по элементарным функциям. Коэффициентами этого разложения являются те же случайные величины V x , V 2 , ..., V m , а математическое ожидание и координатные функции получены из математического ожидания и координатных функций исходной случайной функции тем же линейным преобразованием L, какому подвергается случайная функция У (О-

Резюмируя, получаем следующее правило преобразования случайной функции, заданной разложением.

Если случайная функция X(t), заданная разложением по элементарным функциям, подвергается линейному преобразованию L, то коэффициенты разложения остаются неизменными, а математическое ожидание и координатные функции подвергаются тому же линейному преобразованию L.

Таким образом, смысл представления случайной функции в виде разложения сводится к тому, чтобы свести линейное преобразование случайной функции к таким же линейным преобразованиям нескольких неслучайных функций - математического ожидания и координатных функций. Это позволяет значительно упростить решение задачи нахождения характеристик случайной функции Y(t) по сравнению с общим решением, данным в подразделе 15.7. Действительно, каждая из неслучайных функций m x (t), ф, (7), ф 2 (/), ..., ..., Ф,„(Г) в данном случае преобразуется только один раз в отличие от корреляционной функции K x (t, /"), которая согласно общим правилам преобразуется дважды.

Пусть непрерывный центрированный случайный процесс задан каноническим разложением

, (1.21)

где - некоррелированные случайные коэффициенты с параметрами - система некоторых детерминированных координатных функций.

Из условия некоррелированности коэффициентов , следует аналогичное каноническое разложение корреляционной функции случайного процесса :

. (1.22)

Задание случайного процесса в виде канонического разложения - это и есть параметрическое задание случайного процесса, о котором шла речь в § 1.1.

Моделирование случайного процесса, заданного каноническим разложением, осуществляется довольно просто: в процессе формирования дискретных реализаций (в процессе выработки координат случайного вектора) они вычисляются по формуле (1.21) непосредственно. При этом в качестве используются выборочные значения некоррелированных случайных величин с параметрами . Бесконечный ряд. (1.21) при вычислениях приближенно заменяется усеченным конечным рядом.

Подготовительная работа при моделировании случайных векторов методом канонических разложений заключается в выборе системы координатных функций и в нахождении дисперсий , т. е. в осуществлении непосредственно канонического разложения. Часто в качестве координатных функций выбирают систему ортонормированных функций, т. е. функций, удовлетворяющих условию

Разложение случайного процесса в ряд с некоррелированными коэффициентами по ортонормированной системе функций всегда может быть произведено (теорема Карунена - Лоева). При этом дисперсии находятся как собственные значения, а функции - как собственные функции интегрального уравнения

, (1.23)

где - интервал разложения (в том числе и ); – произвольная неотрицательная функция веса.

К сожалению, разложение (1.21), полученное с помощью (1.23), больше применяется при теоретических исследованиях, а практическое использование его затруднено, так как не существует достаточно простого общего способа решения интегральных уравнений вида (1.23). Сравнительно несложное решение можно получить лишь в некоторых специальных случаях, например для стационарных случайных процессов с рациональной спектральной плотностью.

Существуют приближенные способы получения канонических разложений случайных процессов. Среди них наиболее удобным для моделирования случайных векторов и случайных процессов является способ канонического разложения случайных функций в дискретном ряде точек, предложенный В. С. Пугачевым. Описание этого способа и порядок его практического использования дается в . Мы приведем здесь лишь окончательный алгоритм вычисления дисперсий некоррелированных случайных коэффициентов и координатных функций в разложении (1.21).

Пусть задан случайный процесс с корреляционной функцией и пусть на временной оси задана последовательность точек , (не обязательно равностоящих). Требуется аппроксимировать случайный процесс случайным процессом , представленным в виде разложения (1.21) и таким, что его корреляционная функция совпадает с в заданных дискретных точках, т. е.

Такому условию, как показано в , удовлетворяет каноническое разложение с конечным числом слагаемых, равным числу дискретных точек :

, (1.24)

причем дисперсии коэффициентов и координатные функции в разложении (1.24) могут быть найдены по следующим рекуррентным формулам:

(1.25)

Существенным достоинством данного способа является то, что он позволяет получить каноническое разложение с помощью обычных алгебраических операций, не прибегая к решению интегральных уравнений, и особенно удобен при небольшом числе дискретных точек. При большом числе дискретных точек данный способ требует довольно громоздких вычислений.

Корреляционная функция случайного процесса, каноническое разложение которого получается по формулам (1.26), в промежутках между дискретными точками, вообще говоря, не совпадает с корреляционной функцией исходного процесса. Однако если дискретные точки выбираются так, что значения процесса в этих точках имеют высокую корреляцию между собой, то совпадение корреляционных функций в промежуточных точках будет достаточно хорошим. Это позволяет использовать процесс не только для формирования значений процесса в заданных дискретных точках, но и в промежуточных точках.

Пусть требуется формировать на ЦВМ значения процесса только в заданных дискретных точках , т. е. требуется получать выборочные значения -мерного вектора

с корреляционной матрицей

где - корреляционная функция дискретного случайного процесса . Используя данное каноническое разложение, получим следующий моделирующий алгоритм:

, (1.26)

в котором дисперсии некоррелированных случайных коэффициентов и дискретные координатные функции находятся из соотношений:

(1.27)

Алгоритм (1.26) можно записать в виде

, (1.28)

где - некоррелированные случайные величины с параметрами (0,1).

Если моделируемый процесс является нормальным, то, положив закон распределения случайных коэффициентов в каноническом разложении по данному способу нормальным, придем к алгоритму, позволяющему точно, т. е. в рамках многомерных распределений, а не в рамках корреляционных приближений, формировать на ЦВМ дискретные реализации стационарных и нестационарных нормальных случайных процессов, заданных на конечном интервале времени.

При формировании по этому способу реализаций случайных векторов подготовительная работа по объему вычислительных затрат примерно такая же, что и при формировании случайных векторов с помощью линейного преобразования, описанного выше. Однако необходимое количество ячеек памяти в данном способе может быть значительно меньшим. Это имеет место в тех случаях, когда координатные функции удается выразить достаточно простыми аналитическими выражениями. В противном случае значения и т. д.

Таким образом, формулы (1.27) являются разновидностью формул (1.19) для вычисления элементов матрицы преобразования .

Лекция 14 Случайные процессы Каноническое разложение случайных процессов. Спектральное разложение стационарного случайного процесса. СлуЛекция 14
Случайные процессы
Каноническое разложение случайных процессов.
Спектральное разложение стационарного случайного
процесса. Случайные процессы с независимыми
сечениями. Марковские процессы и цепи Маркова.
Нормальные случайные процессы. Периодически
нестационарные случайные процессы
(Ахметов С.К.)

Каноническое разложение случайных процессов

Любой СП X(t) м.б. представлен в
виде его разложения, т.е. в виде суммы
элементарных процессов:
Vk – случайные величины
φk(t) – неслучайные функции (синусоиды, экспоненты, степенные
функции и т.д)
Частный случай такого разложения-Каноническое
разложение
СП X(t), имеющее вид
mx(t) = M – математическое ожидание СП X(t)
V1, V2…Vk – некоррелированные и центрированные СВ
D1, D2 …Dk- дисперсии СВ V1, V2…Vk
φk(t) – неслучайные функции аргумента t
Случайные величины V1, V2…Vk называются коэффициентами канонического
разложения,
а неслучайные функции φ1(t), φ2(t) φk(t) - координатными функциями
канонического разложения

Основные характеристики СП, заданного каноническим разложением

M – математическое ожидание СП X(t)
Kx(t,t’) – корреляционная функция СП X(t)
Выражение
- каноническое разложение корреляционной
функции
Если t=t’, то в соответствие с первым
свойством корреляционной функции
Выражение
Dk(t) –
дисперсия
каноническое разложение дисперсии СП X(t)

Спектральное разложение стационарного СП

Стационарный СП м.б. представлен каноническим разложением
Vk и Uk – некоррелированные и центрированные СВ с дисперсиями
D = D = Dk
ω – неслучайная величина (частота)
В этом случае каноническое разложение корреляционной функции
определяется выражением
Представленное
каноническое
разложение
СП
X(t)
называется
спектральным разложением СП и
выражается в виде
Θk - фаза гармонического колебания элементарного стационарного СП,
являющаяся СВ равномерно распределенной в интервале (0, 2π);
Zk – СВ, представляющая собой амплитуду гармонического колебания
элементарного стационарного СП

Спектральное разложение стационарного СП (2)

Случайные величины Θk и Zk зависимы и для них справедливо:
Vk = Zk cos Θk
Uk = Zk sin Θk
Стационарный СП м.б. представлен в виде суммы гармонических
колебаний со случайными амплитудами Zk и случайными фазами Θk на
различных неслучайных частотах ωk
Корреляционная функция стационарного СП X(t) является четной
функцией своего аргумента, т.е. kx(τ) = kx(-τ). Поэтому ее на интервале (-Т,
Т) можно разложить в ряд Фурье по четным (косинусам) гармоникам:
Дисперсия стационарного СП X(t) равна
сумме
дисперсий
всех
гармоник
его
спектрального разложения
Зависимость Dk = f(wk) называется дискретным спектром дисперсий или
дискретным спектром стационарного СП.

Спектральное разложение стационарного СП (3)

При ∆ω
→ 0 произойдет переход к непрерывному спектру
Sx(ω) - спектральная плотность
Таким образом, корреляционная функция и спектральная плотность
связаны косинус – преобразованием Фурье. Следовательно, спектральная
плотность стационарного СП м.б. выражена через корреляционную
функцию формулой

Случайные процессы с независимыми сечениями

В гидрологии считается, что ряд соответствует модели случайной
величины, если отсутствует значимая корреляция между членами этого ряда
при любом сдвиге τ.
Случайный процесс с независимыми сечениями – это СП, для которого
при значениях t и t’
mx(t) = mx
Dx (t) = Dx
Kx(t,t’) = kx(τ) = {Dx при τ = 0 и 0 при τ ≠ 0}
Такой процесс является стационарным и обладает эргодическим
свойством
Для таких процессов характеристики одномерного закона распределения
можно оценить как по любому сечению, так и по любой (достаточно
продолжительной) реализации
У таких процессов отсутствует корреляция между членами внутри любой
реализации
Принимая такую модель, допускается, что ряд гидрологических величин
представляет собой одну реализацию СП
Случайный процесс с независимыми сечениями иногда называют
«белым шумом» по аналогии с белым светом

Марковские процессы и цепи Маркова

Случайный процесс
называется марковским, если для любого
момента времени t вероятность каждого из состояний системы в будущем
(при t > t0) зависит только от ее состояния в настоящем (при t = t0) и не
зависит от ее состояния в прошлом (при t < t0)
Марковской цепью или простой марковской цепью называется
марковский процесс с дискретным состоянием и дискретным временем
Марковский СП полностью описывается двумерным законом
распределения. Если Марковский процесс является стационарным и
эргодическим, то его характеристики можно оценить по одной
реализации.
Цепь, в которой условные вероятности состояний в будущем зависят
от ее состояния на нескольких предыдущих шагах, называется сложной
цепью Маркова.

Нормальные (Гауссовские) случайные процессы

Нормальным (гауссовским) случайным процессом X(t) называется
СП, у которого во всех сечениях СВ X(ti) имеет нормальное
распределение
Периодически нестационарные СП
При изучении годовых, месячных, суточных и т.д. процессов, обычно,
наблюдаются внутригодовые и т.д. колебания. В этом случае, в качестве
математической модели можно использовать модель периодически
нестационарного случайного процесса (ПНСП)
Случайный процесс называют периодически нестационарным, если
его вероятностные характеристики инварианты относительно сдвигов на
положительное число Т. Например, при шаге дискретности один месяц
инвариантность должна сохраняться при сдвигах 12, 24, 36 и т.д.