Формула для определения частоты колебаний. Формула частоты. Связь между периодом и круговой частотой

При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.

Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.

Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.

Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна - это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

Таблица формул: колебания и волны

(лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.

Для маятника это максимальное расстояние, на которое удаляется ша-рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах , санти-метрах и т. д. На графике колебаний амплитуда определяется как макси-мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.

Период колебаний — это наименьший промежуток времени, через который система, соверша-ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.

Другими словами, период колебаний (Т ) — это время, за которое совершается одно полное ко-лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четы-рем амплитудам. Период колебаний измеряется в единицах времени — секундах , минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей-ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес-ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю-щихся величин, например, для затухающих колебаний .

Частота колебаний.

Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с .

Единица частоты в СИ названа герцем (Гц ) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v ) равна 1 Гц , то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической , или круговой частоты ω . Она связана с обычной частотой v и периодом колебаний Т соотношениями:

.

Циклическая частота — это число колебаний, совершаемых за 2π секунд.

Гармонические колебания – колебания, совершаемые по законам синуса и косинуса. На следующем рисунке представлен график изменения координаты точки с течением времени по закону косинуса.

картинка

Амплитуда колебаний

Амплитудой гармонического колебания называется наибольшее значение смещения тела от положения равновесия. Амплитуда может принимать различные значения. Она будет зависеть от того, насколько мы сместим тело в начальный момент времени от положения равновесия.

Амплитуда определяется начальными условиями, то есть энергией сообщаемой телу в начальный момент времени. Так как синус и косинус могут принимать значения в диапазоне от -1 до 1, то в уравнении должен присутствовать множитель Xm, выражающий амплитуду колебаний. Уравнение движения при гармонических колебаниях:

x = Xm*cos(ω0*t).

Период колебаний

Период колебаний – это время совершения одного полного колебания. Период колебания обозначается буквой Т. Единицы измерения периода соответствуют единицам времени. То есть в СИ - это секунды.

Частота колебаний – количество колебаний совершенных в единицу времени. Частота колебаний обозначается буквой ν. Частоту колебаний можно выразить через период колебания.

ν = 1/Т.

Единицы измерения частоты в СИ 1/сек. Эта единица измерения получила название Герца. Число колебаний за время 2*pi секунд будет равняться:

ω0 = 2*pi* ν = 2*pi/T.

Частота колебаний

Данная величина называется циклической частотой колебаний. В некоторой литературе встречается название круговая частота. Собственная частота колебательной системы – частота свободных колебаний.

Частота собственных колебаний рассчитывается по формуле:

Частота собственных колебаний зависит от свойств материала и массы груза. Чем больше жесткость пружины, тем больше частота собственных колебаний. Чем больше масса груза, тем меньше частота собственных колебаний.

Эти два вывода очевидны. Чем более жесткая пружина, тем большее ускорение она сообщит телу, при выведении системы из равновесия. Чем больше масса тела, тем медленнее будет изменяться это скорость этого тела.

Период свободных колебаний :

T = 2*pi/ ω0 = 2*pi*√(m/k)

Примечателен тот факт, что при малых углах отклонения период колебания тела на пружине и период колебания маятника не будут зависеть от амплитуды колебаний.

Запишем формулы периода и частоты свободных колебаний для математического маятника.

тогда период будет равен

T = 2*pi*√(l/g).

Данная формула будет справедлива лишь для малых углов отклонения. Из формулы видим, что период колебаний возрастает с увеличением длины нити маятника. Чем больше будет длина, тем медленнее тело будет колебаться.

От массы груза период колебаний совершенно не зависит. Зато зависит от ускорения свободного падения. При уменьшении g, период колебаний будет увеличиваться. Данное свойство широко используют на практике. Например, для измерения точного значения свободного ускорения.

Колебательным называется любое периодически повторяющееся движение. Поэтому зависимости координаты и скорости тела от времени при колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются такие колебания, в которых зависимости и скорости тела представляют собой тригонометрические функции , или их комбинацию, где - некоторое число. Такие колебания на-зываются гармоническими (функции и часто называют гармоническими функциями). Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени , которая в случае гармонических колебаний всегда может быть представлена в виде

где , и - некоторые числа.

Амплитудой колебаний называется максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значение косинуса в (11.1) равно ±1, то амплитуда колебаний тела, совершающего колебания (11.1), равна величине . Период колебаний - это минимальное время, через которое движение тела повторяется. Для зависимости (11.1) период можно установить из следующих соображений. Косинус - периодическая функция с периодом . Поэтому движение полностью повторяется через такое значение , что . Отсюда получаем

Круговой (или циклической) частотой колебаний называется число колебаний, совершаемых за единиц времени. Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).

Фазой колебаний называется аргумент тригонометрической функции, описывающей зависимость координаты от времени. Из формулы (11.1) видим, что фаза колебаний тела, движение которого описывается зависимостью (11.1), равна . Значение фазы колебаний в момент времени = 0 называется начальной фазой. Для зависимости (11.1) начальная фаза колебаний равна величине . Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента = 0), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот.

В программу единого государственного экзамена входит также знание формул для частоты колебаний пружинного и математического маятников. Пружинным маятником принято называть тело, которое может совершать колебания на гладкой горизонтальной поверхности под действием пружины, второй конец которой закреплен (левый рисунок). Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического ) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника

где - длина нити, - ускорение свободного падения. Рассмотрим применение этих определений и законов на примере решения задач.

Чтобы найти циклическую частоту колебаний груза в задаче 11.1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с - это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c -1 (ответ 2 ). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний - 0,1 с -1 (ответ 1 ).

Чтобы понять, какой путь пройдет груз за 2,5 периода (задача 11.1.3 ), проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия - одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону - вторая, назад в положение равновесия - третья, из положения равновесия в начальную точку - четвертая. За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода - две амплитуды. Поэтому пройденный путь равен десяти амплитудам (ответ 4 ).

Величина перемещения тела - расстояние от начальной точки до конечной. За 2,5 периода в задаче 11.1.4 тело успеет совершить два полных и половину полного колебания, т.е. окажется на максимальном отклонении, но с другой стороны от положения равновесия. Поэтому величина перемещения равна двум амплитудам (ответ 3 ).

По определению фаза колебаний - это аргумент тригонометрической функции, которой описывается зависимость координаты колеблющегося тела от времени. Поэтому правильный ответ в задаче 11.1.5 - 3 .

Период - это время полного колебания. Это значит, что возвращение тела назад в ту же точку, из которой тело начало движение, еще не означает, что прошел период: тело должно вернуться в ту же точку с той же скоростью. Например, тело, начав колебания из положения равновесия, за период успеет отклониться на максимальную величину в одну сторону, вернуться назад, отклонится на максимум в другую сторону и снова вернуться назад. Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (задача 11.1.6 ) тело затрачивает четвертую часть периода (ответ 3 ).

Гармоническими называются такие колебания, при которых зависимость координаты колеблющегося тела от времени описывается тригонометрической (синус или косинус) функцией времени. В задаче 11.1.7 таковыми являются функции и , несмотря на то, что входящие в них параметры обозначены как 2 и 2 . Функция же - тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин и (ответ 4 ).

При гармонических колебаниях скорость тела изменяется по закону , где - амплитуда колебаний скорости (начало отсчета времени выбрано так, чтобы начальная фаза колебаний равнялась бы нулю). Отсюда находим зависимость кинетической энергии тела от времени
(задача 11.1.8 ). Используя далее известную тригонометрическую формулу, получаем

Из этой формулы следует, что кинетическая энергия тела изменяется при гармонических колебаниях также по гармоническому закону, но с удвоенной частотой (ответ 2 ).

За соотношением между кинетической энергий груза и потенциальной энергией пружины (задача 11.1.9 ) легко проследить из следующих соображений. Когда тело отклонено на максимальную величину от положения равновесия, скорость тела равна нулю, и, следовательно, потенциальная энергия пружины больше кинетической энергии груза. Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза (ответ 2 ).

Амплитуду колебаний скорости (задача 11.1.10 ) проще всего найти по закону сохранения энергии. В точке максимального отклонения энергия колебательной системы равна потенциальной энергии пружины , где - коэффициент жесткости пружины, - амплитуда колебаний. При прохождении положения равновесия энергия тела равна кинетической энергии , где - масса тела, - скорость тела при прохождении положения равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебаний скорости. Приравнивая эти энергии, находим

(ответ 4 ).

Из формулы (11.5) заключаем (задача 11.2.2 ), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1 ).

Часы - это колебательный процесс, который используется для измерения интервалов времени (задача 11.2.3 ). Слова часы «спешат» означают, что период этого процесса меньше того, каким он должен быть. Поэтому для уточнения хода этих часов необходимо увеличить период процесса. Согласно формуле (11.5) для увеличения периода колебаний математического маятника необходимо увеличить его длину (ответ 3 ).

Чтобы найти амплитуду колебаний в задаче 11.2.4 , необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на и используя формулу сложения тригонометрических функций, получим

где - такой угол, что . Из этой формулы следует, что амплитуда колебаний тела - (ответ 4 ).

1. Механические волны, частота волны. Продольные и поперечные волны.

2. Волновой фронт. Скорость и длина волны.

3. Уравнение плоской волны.

4. Энергетические характеристики волны.

5. Некоторые специальные разновидности волн.

6. Эффект Доплера и его использование в медицине.

7. Анизотропия при распространении поверхностных волн. Действие ударных волн на биологические ткани.

8. Основные понятия и формулы.

9. Задачи.

2.1. Механические волны, частота волны. Продольные и поперечные волны

Если в каком-либо месте упругой среды (твердой, жидкой или газообразной) возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде от частицы к частице с некоторой скоростью v.

Например, если в жидкую или газообразную среду поместить колеблющееся тело, то колебательное движение тела будет передаваться прилегающим к нему частицам среды. Они, в свою очередь, вовлекают в колебательное движение соседние частицы и так далее. При этом все точки среды совершают колебания с одинаковой частотой, равной частоте колебания тела. Эта частота называется частотой волны.

Волной называется процесс распространения механических колебаний в упругой среде.

Частотой волны называется частота колебаний точек среды, в которой распространяется волна.

С волной связан перенос энергии колебаний от источника колебаний к периферийным участкам среды. При этом в среде возникают

периодические деформации, которые переносятся волной из одной точки среды в другую. Сами частицы среды не перемещаются вместе с волной, а колеблются около своих положений равновесия. Поэтому распространение волны не сопровождается переносом вещества.

В соответствии с частотой механические волны делятся на различные диапазоны, которые указаны в табл. 2.1.

Таблица 2.1. Шкала механических волн

В зависимости от направления колебаний частиц по отношению к направлению распространения волны, различают продольные и поперечные волны.

Продольные волны - волны, при распространении которых частицы среды колеблются вдоль той же прямой, по которой распространяется волна. При этом в среде чередуются области сжатия и разряжения.

Продольные механические волны могут возникать во всех средах (твердых, жидких и газообразных).

Поперечные волны - волны, при распространении которых частицы колеблются перпендикулярно направлению распространения волны. При этом в среде возникают периодические деформации сдвига.

В жидкостях и газах упругие силы возникают только при сжатии и не возникают при сдвиге, поэтому поперечные волны в этих средах не образуются. Исключение составляют волны на поверхности жидкости.

2.2. Волновой фронт. Скорость и длина волны

В природе не существует процессов, распространяющихся с бесконечно большой скоростью, поэтому возмущение, созданное внешним воздействием в одной точке среды, достигнет другой точки не мгновенно, а спустя некоторое время. При этом среда делится на две области: область, точки которой уже вовлечены в колебательное движение, и область, точки которой еще находятся в равновесии. Поверхность, разделяющая эти области, называется фронтом волны.

Фронт волны - геометрическое место точек, до которых к данному моменту дошло колебание (возмущение среды).

При распространении волны ее фронт перемещается, двигаясь с некоторой скоростью, которую называют скоростью волны.

Скоростью волны (v) называется скорость перемещения ее фронта.

Скорость волны зависит от свойств среды и типа волны: поперечные и продольные волны в твердом теле распространяются с различными скоростями.

Скорость распространения всех типов волн определяется при условии слабого затухания волны следующим выражением:

где G - эффективный модуль упругости, ρ - плотность среды.

Скорость волны в среде не следует путать со скоростью движения частиц среды, вовлеченных в волновой процесс. Например, при распространении звуковой волны в воздухе средняя скорость колебаний его молекул порядка 10 см/с, а скорость звуковой волны при нормальных условиях около 330 м/с.

Форма волнового фронта определяет геометрический тип волны. Простейшие типы волн по этому признаку - плоские и сферические.

Плоской называется волна, у которой фронтом является плоскость, перпендикулярная направлению распространения.

Плоские волны возникают, например, в закрытом поршнем цилиндре с газом, когда поршень совершает колебания.

Амплитуда плоской волны остается практически неизменной. Ее слабое уменьшение по мере удаления от источника волны связано с вязкостью жидкой или газообразной среды.

Сферической называется волна, у которой фронт имеет форму сферы.

Такой, например, является волна, вызываемая в жидкой или газообразной среде пульсирующим сферическим источником.

Амплитуда сферической волны при удалении от источника убывает обратно пропорционально квадрату расстояния.

Для описания ряда волновых явлений, например интерференции и дифракции, используют специальную характеристику, называемую длиной волны.

Длиной волны называется расстояние, на которое перемещается ее фронт за время, равное периоду колебаний частиц среды:

Здесь v - скорость волны, Т - период колебаний, ν - частота колебаний точек среды, ω - циклическая частота.

Так как скорость распространения волны зависит от свойств среды, то длина волны λ при переходе из одной среды в другую изменяется, в то время как частота ν остается прежней.

Данное определение длины волны имеет важную геометрическую интерпретацию. Рассмотрим рис. 2.1 а, на котором показаны смещения точек среды в некоторый момент времени. Положение фронта волны отмечено точками А и В.

Через время Т, равное одному периоду колебаний, фронт волны переместится. Его положения показаны на рис. 2.1, б точками А 1 и В 1 . Из рисунка видно, что длина волны λ равна расстоянию между соседними точками, колеблющимися в одинаковой фазе, например расстоянию между двумя соседними максимумами или минимумами возмущения.

Рис. 2.1. Геометрическая интерпретация длины волны

2.3. Уравнение плоской волны

Волна возникает в результате периодических внешних воздействий на среду. Рассмотрим распространение плоской волны, созданной гармоническими колебаниями источника:

где х и - смещение источника, А - амплитуда колебаний, ω - круговая частота колебаний.

Если некоторая точка среды удалена от источника на расстояние s, а скорость волны равна v, то возмущение, созданное источником, достигнет этой точки через время τ = s/v. Поэтому фаза колебаний в рассматриваемой точке в момент времени t будет такой же, как фаза колебаний источника в момент времени (t - s/v), а амплитуда колебаний останется практически неизменной. В результате колебания данной точки будут определяться уравнением

Здесь мы использовали формулы для круговой частоты (ω = 2π/Т) и длины волны (λ = v T).

Подставив это выражение в исходную формулу, получим

Уравнение (2.2), определяющее смещение любой точки среды в любой момент времени, называется уравнением плоской волны. Аргумент при косинусе - величина φ = ωt - 2π s/λ - называется фазой волны.

2.4. Энергетические характеристики волны

Среда, в которой распространяется волна, обладает механической энергией, складывающейся из энергий колебательного движения всех ее частиц. Энергия одной частицы с массой m 0 находится по формуле (1.21): Е 0 = m 0 Α 2 ω 2 /2. В единице объема среды содержится n = p /m 0 частиц (ρ - плотность среды). Поэтому единица объема среды обладает энергией w р = nЕ 0 = ρ Α 2 ω 2 /2.

Объемная плотность энергии (\¥ р) - энергия колебательного движения частиц среды, содержащихся в единице ее объема:

где ρ - плотность среды, А - амплитуда колебаний частиц, ω - частота волны.

При распространении волны энергия, сообщаемая источником, переносится в удаленные области.

Для количественного описания переноса энергии вводят следующие величины.

Поток энергии (Ф) - величина, равная энергии, переносимой волной через данную поверхность за единицу времени:

Интенсивность волны или плотность потока энергии (I) - величина, равная потоку энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны:

Можно показать, что интенсивность волны равна произведению скорости ее распространения на объемную плотность энергии

2.5. Некоторые специальные разновидности

волн

1. Ударные волны. При распространении звуковых волн скорость колебания частиц не превышает нескольких см/с, т.е. она в сотни раз меньше скорости волны. При сильных возмущениях (взрыв, движение тел со сверхзвуковой скоростью, мощный электрических разряд) скорость колеблющихся частиц среды может стать сравнимой со скоростью звука. При этом возникает эффект, называемый ударной волной.

При взрыве нагретые до высоких температур продукты, обладающие большой плотностью, расширяются и сжимают тонкий слой окружающего воздуха.

Ударная волна - распространяющаяся со сверхзвуковой скоростью тонкая переходная область, в которой происходит скачкообразное возрастание давления, плотности и скорости движения вещества.

Ударная волна может обладать значительной энергией. Так, при ядерном взрыве на образование ударной волны в окружающей среде затрачивается около 50 % всей энергии взрыва. Ударная волна, достигая объектов, способна вызвать разрушения.

2. Поверхностные волны. Наряду с объемными волнами в сплошных средах при наличии протяженных границ могут существовать волны, локализованные вблизи границ, которые играют роль волноводов. Таковы, в частности, поверхностные волны в жидкости и упругой среде, открытые английским физиком В. Стреттом (лордом Релеем) в 90-х годах 19 века. В идеальном случае волны Релея распространяются вдоль границы полупространства, экспоненциально затухая в поперечном направлении. В результате поверхностные волны локализуют энергию возмущений, созданных на поверхности, в сравнительно узком приповерхностном слое.

Поверхностные волны - волны, которые распространяются вдоль свободной поверхности тела или вдоль границы тела с другими средами и быстро затухают при удалении от границы.

Примером таких волн могут служить волны в земной коре (сейсмические волны). Глубина проникновения поверхностных волн составляет несколько длин волн. На глубине, равной длине волны λ, объемная плотность энергии волны составляет приблизительно 0,05 ее объемной плотности на поверхности. Амплитуда смещения быстро убывает при удалении от поверхности и на глубине нескольких длин волн практически исчезает.

3. Волны возбуждения в активных средах.

Активно возбудимая, или активная, среда - непрерывная среда, состоящая из большого числа элементов, каждый из которых обладает запасом энергии.

При этом каждый элемент может находиться в одном из трех состояний: 1 - возбуждение, 2 - рефрактерность (невозбудимость в течение определенного времени после возбуждения), 3 - покой. В возбуждение могут перейти элементы только из состояния покоя. Волны возбуждения в активных средах называют автоволнами. Автоволны - это самоподдерживающиеся волны в активной среде, сохраняющие свои характеристики постоянными за счет распределенных в среде источников энергии.

Характеристики автоволны - период, длина волны, скорость распространения, амплитуда и форма - в установившемся режиме зависят только от локальных свойств среды и не зависят от начальных условий. В табл. 2.2 представлено сходство и различие автоволн и обычных механических волн.

Автоволны можно сопоставить с распространением пожара в степи. Пламя распространяется по области с распределенными запасами энергии (по сухой траве). Каждый последующий элемент (сухая травинка) зажигается от предыдущего. И таким образом распространяется фронт волны возбуждения (пламя) по активной среде (сухой траве). При встрече двух очагов пожара пламя исчезает, так как исчерпаны запасы энергии - вся трава выгорела.

Описание процессов распространения автоволн в активных средах используется при изучении распространения потенциалов действия по нервным и мышечным волокнам.

Таблица 2.2. Сравнение автоволн и обычных механических волн

2.6. Эффект Доплера и его использование в медицине

Христиан Доплер (1803-1853) - австрийский физик, математик, астроном, директор первого в мире физического института.

Эффект Доплера состоит в изменении частоты колебаний, воспринимаемой наблюдателем, вследствие относительного движения источника колебаний и наблюдателя.

Эффект наблюдается в акустике и оптике.

Получим формулу, описывающую эффект Доплера, для случая, когда источник и приемник волны движутся относительно среды вдоль одной прямой со скоростями v И и v П соответственно. Источник совершает гармонические колебания с частотой ν 0 относительно своего равновесного положения. Волна, созданная этими колебаниями, распространяется в среде со скоростью v. Выясним, какую частоту колебаний зафиксирует в этом случае приемник.

Возмущения, создаваемые колебаниями источника, распространяются в среде и достигают приемника. Рассмотрим одно полное колебание источника, которое начинается в момент времени t 1 = 0

и заканчивается в момент t 2 = T 0 (T 0 - период колебаний источника). Возмущения среды, созданные в эти моменты времени, достигают приемника в моменты t" 1 и t" 2 соответственно. При этом приемник фиксирует колебания с периодом и частотой:

Найдем моменты t" 1 и t" 2 для случая, когда источник и приемник движутся навстречу друг другу, а начальное расстояние между ними равно S. В момент t 2 = T 0 это расстояние станет равным S - (v И + v П)T 0 , (рис. 2.2).

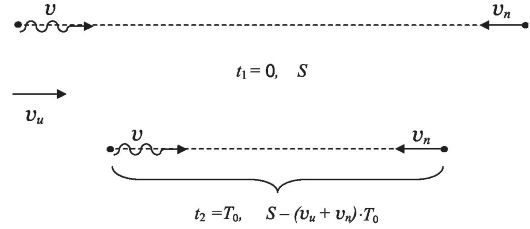Рис. 2.2. Взаимное расположение источника и приемника в моменты t 1 и t 2

Эта формула справедлива для случая, когда скорости v и и v п направлены навстречу друг другу. В общем случае при движении

источника и приемника вдоль одной прямой формула для эффекта Доплера принимает вид

Для источника скорость v И берется со знаком «+», если он движется в направлении приемника, и со знаком «-» в противном случае. Для приемника - аналогично (рис. 2.3).

Рис. 2.3. Выбор знаков для скоростей источника и приемника волн

Рассмотрим один частный случай использования эффекта Доплера в медицине. Пусть генератор ультразвука совмещен с приемником в виде некоторой технической системы, которая неподвижна относительно среды. Генератор излучает ультразвук, имеющий частоту ν 0 , который распространяется в среде со скоростью v. Навстречу системе со скоростью v т движется некоторое тело. Сначала система выполняет роль источника (v И = 0), а тело - роль приемника (v Tl = v Т). Затем волна отражается от объекта и фиксируется неподвижным приемным устройством. В этом случае v И = v Т, а v п = 0.

Применив формулу (2.7) дважды, получим формулу для частоты, фиксируемой системой после отражения испущенного сигнала:

При приближении объекта к датчику частота отраженного сигнала увеличивается, а при удалении - уменьшается.

Измерив доплеровский сдвиг частоты, из формулы (2.8) можно найти скорость движения отражающего тела:

Знак «+» соответствует движению тела навстречу излучателю.

Эффект Доплера используется для определения скорости кровотока, скорости движения клапанов и стенок сердца (доплеровская эхокардиография) и других органов. Схема соответствующей установки для измерения скорости крови показана на рис. 2.4.

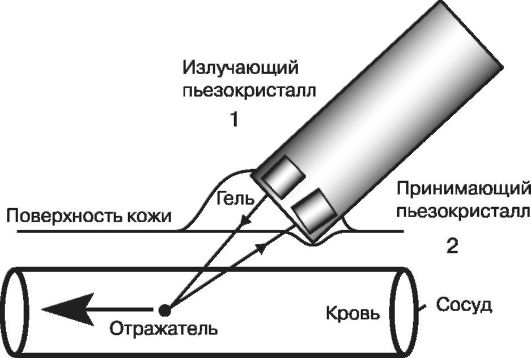Рис. 2.4. Схема установки для измерения скорости крови: 1 - источник ультразвука, 2 - приемник ультразвука

Установка состоит из двух пьезокристаллов, один из которых служит для генерации ультразвуковых колебаний (обратный пьезоэффект), а второй - для приема ультразвука (прямой пьезоэффект), рассеянного кровью.

Пример . Определить скорость кровотока в артерии, если при встречном отражении ультразвука (ν 0 = 100 кГц = 100 000 Гц, v = 1500 м/с) от эритроцитов возникает доплеровский сдвиг частоты ν Д = 40 Гц.

Решение. По формуле (2.9) найдем:

v 0 = v Д v /2v 0 = 40x 1500/(2x 100 000) = 0,3 м/с.

2.7. Анизотропия при распространении поверхностных волн. Действие ударных волн на биологические ткани

1. Анизотропия распространения поверхностных волн. При исследовании механических свойств кожи с помощью поверхностных волн на частоте 5-6 кГц (не путать с УЗ) проявляется акустическая анизотропия кожи. Это выражается в том, что скорости распространения поверхностной волны во взаимно перпендикулярных направлениях - вдоль вертикальной (Y) и горизонтальной (Х) осей тела - различаются.

Для количественной оценки степени выраженности акустической анизотропии используется коэффициент механической анизотропии, который вычисляется по формуле:

где v у - скорость вдоль вертикальной оси, v x - вдоль горизонтальной оси.

Коэффициент анизотропии принимается за положительный (К+), если v y > v x при v y < v x коэффициент принимается за отрицательный (К -). Численные значения скорости поверхностных волн в коже и степени выраженности анизотропии являются объективными критериями для оценки различных воздействий, в том числе и на кожу.

2. Действие ударных волн на биологические ткани. Во многих случаях воздействия на биологические ткани (органы) необходимо учитывать возникающие при этом ударные волны.

Так, например, ударная волна возникает при ударе тупым предметом по голове. Поэтому при проектировании защитных касок заботятся о том, чтобы погасить ударную волну и предохранить затылок при лобовом ударе. Этой цели и служит внутренняя лента в каске, которая на первый взгляд кажется необходимой лишь для вентиляции.

Ударные волны возникают в тканях при воздействии на них высокоинтенсивного лазерного излучения. Часто после этого в коже начинают развиваться рубцовые (или иные) изменения. Это, например, имеет место в косметологических процедурах. Поэтому, для того чтобы снизить вредное воздействие ударных волн, необходимо заранее рассчитывать дозирование воздействия с учетом физических свойств как излучения, так и самой кожи.

Рис. 2.5. Распространение радиальных ударных волн

Ударные волны используются в радиальной ударно-волновой терапии. На рис. 2.5 показано распространение радиальных ударных волн от аппликатора.

Такие волны создаются в приборах, снабженных специальным компрессором. Радиальная ударная волна генерируется пневматическим методом. Поршень, находящийся в манипуляторе, двигается с большой скоростью под воздействием управляемого импульса сжатого воздуха. Когда поршень ударяет по аппликатору, установленному в манипуляторе, его кинетическая энергия превращается в механическую энергию области тела, на которую оказывалось воздействие. При этом для снижения потерь при передаче волн в воздушной прослойке, находящейся между аппликатором и кожей, и для обеспечения хорошей проводимости ударных волн используется контактный гель. Обычный режим работы: частота 6-10 Гц, рабочее давление 250 кПа, число импульсов за сеанс - до 2000.

1. На корабле включают сирену, подающую сигналы в тумане, и спустя t = 6,6 с слышно эхо. Как далеко находится отражающая поверхность? Скорость звука в воздухе v = 330 м/с.

Решение

За время t звук проходит путь 2S: 2S = vt →S = vt/2 = 1090 м. Ответ: S = 1090 м.

2. Каков минимальный размер предметов, положение которых могут определить летучие мыши с помощью своего сенсора, имеющего частоту 100 000 Гц? Каков минимальный размер предметов, которые могут обнаружить дельфины с использованием частоты 100 000 Гц?

Решение

Минимальные размеры предмета равны длине волны:

λ 1 = 330 м/с / 10 5 Гц = 3,3 мм. Таков примерно размер насекомых, которыми питаются летучие мыши;

λ 2 = 1500 м/с / 10 5 Гц = 1,5 см. Дельфин может обнаружить небольшую рыбку.

Ответ: λ 1 = 3,3 мм; λ 2 = 1,5 см.

3. Сначала человек видит вспышку молнии, а через 8 с после этого слышит удар грома. На каком расстоянии от него сверкнула молния?

Решение

S = v зв t = 330x 8 = 2640 м. Ответ: 2640 м.

4. Две звуковые волны имеют одинаковые характеристики, за исключением того, что длина волны одной в два раза больше, чем у другой. Которая из них переносит большую энергию? Во сколько раз?

Решение

Интенсивность волны прямо пропорциональна квадрату частоты (2.6) и обратно пропорциональна квадрату длины волны (ω = 2πv/λ). Ответ: та, у которой длина волны меньше; в 4 раза.

5. Звуковая волна, имеющая частоту 262 Гц, распространяется в воздухе со скоростью 345 м/с. а) Чему равна ее длина волны? б) За какое время фаза в данной точке пространства меняется на 90°? в) Чему равна разность фаз (в градусах) между точками, отстоящими друг от друга на 6,4 см?

Решение

а) λ = v/ν = 345/262 = 1,32 м;

в) Δφ = 360°s/λ= 360x 0,064/1,32 = 17,5°. Ответ: а) λ = 1,32 м; б) t = T/4; в) Δφ = 17,5°.

6. Оценить верхнюю границу (частоту) ультразвука в воздухе, если известна скорость его распространения v = 330 м/с. Считать, что молекулы воздуха имеют размер порядка d = 10 -10 м.

Решение

В воздухе механическая волна является продольной и длина волны соответствует расстоянию между двумя ближайшими сгущениями (или разряжениями) молекул. Так как расстояние между сгущениями никак не может быть меньше размеров молекул, то заведомо предельным случаем следует считать d = λ. Из этих соображений имеем ν = v/λ = 3,3x 10 12 Гц. Ответ: ν = 3,3x 10 12 Гц.

7. Две машины движутся навстречу друг другу со скоростями v 1 = 20 м/с и v 2 = 10 м/с. Первая машина подает сигнал с частотой ν 0 = 800 Гц. Скорость звука v = 340 м/с. Какой частоты сигнал услышит водитель второй машины: а) до встречи машин; б) после встречи машин?

8. Когда поезд проходит мимо, Вы слышите, как частота его свистка изменяется от ν 1 = 1000 Гц (при приближении) до ν 2 = 800 Гц (когда поезд удаляется). Чему равна скорость поезда?

Решение

Эта задача отличается от предыдущих тем, что нам неизвестна скорость источника звука - поезда - и неизвестна частота его сигнала ν 0 . Поэтому получается система уравнений с двумя неизвестными:

Решение

Пусть v - скорость ветра, и он дует от человека (приемник) к источнику звука. Относительно земли они неподвижны, а относительно воздушной среды оба движутся вправо со скоростью u.

По формуле (2.7) получим частоту звука. воспринимаемую человеком. Она неизменна:

Ответ: частота не изменится.