Вписанные и описанные многоугольники. Правильные многоугольники
Вписанный в круг многоугольник .
Описанный около круга многоугольник .
Описанный около многоугольника круг .
Вписанный в многоугольник круг .
Радиус вписанного в треугольник круга
.Радиус описанного около треугольника круга
.
Правильный многоугольник
.
Центр
и апофема правильного многоугольника
.
Соотношения сторон и радиусов правильных многоугольников
.
Вписанным в круг называется многоугольник, вершины которого расположены на окружности (рис.54). Описанным около круга называется многоугольник, стороны которого являются касательными к окружности
(рис.55).
Соответственно, окружность, проходящая через вершины многоугольника ( рис.54 ), называется описанной около многоугольника ; окружность, для которой стороны многоугольника являются касательными (рис.55), на зывается вписанной в многоугольник . Для произвольного многоугольника невозможно вписать в него и описать около него окружность. Для треуголь ника это всегда возможно.
Радиус r вписанного круга выражается через стороны a , b , c треугольника:
Радиус R описанного круга выражается формулой:

В четырёхугольник можно вписать окружность, если суммы его противоположных сторон равны. Для параллелограммов это возможно только для ромба (квадрата ). Центр вписанного круга расположен в точке пересечения диагоналей. Около четырёхугольника можно описать круг, если сумма его противоположных углов равна 180º. Для параллелограммов это возможно только для прямоугольника (квадрата ). Центр описанного круга лежит в точке пересечения диагоналей. Вокруг трапеции можно описать круг , если только она равнобочная.
Правильный многоугольник – это многоугольник с равными сторонами и углами.
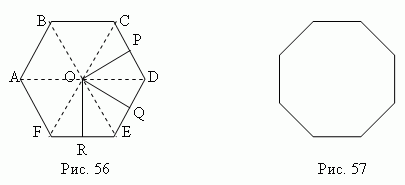
На рис.56 показан правильный шестиугольник, а на рис.57 – правильный восьмиугольник. Правильный четырёхугольник – это квадрат; правильный треугольник – равносторонний треугольник. Каждый угол правильного многоугольника равен 180º (
n – 2) / n , где n – число его углов. Внутри правильного многоугольника существует точка O (рис. 56), равноудалённая от всех его вершин ( OA = OB = OC = … = OF), которая называется центром правильного многоугольника.Центрправильногомногоугольника также равноудалён от всех его сторон ( OP = OQ = OR = …). Отрезки OP, OQ, OR, … называются апофемами ; отрезки OA, OB, OC, …– радиусы правильного многоугольника. В правильный многоугольник можно вписать окружность и около него можно описать окружность. Центры вписанной и описанной окружностей совпадают с центром правильного многоугольника. Радиус описанного круга - это радиус правильного многоугольника, a радиус вписанного круга - его апофема. Соотношения сторон и радиусов правильных многоугольников:
Для большинства правильных многоугольников невозможно выразить посредством алгебраической формулы соотношение между их сторонами и радиусами.
П р и м е р. Можно ли вырезать квадрат со стороной 30 см из круга
Диаметром 40 см?
Р е ш е н и е. Наибольший квадрат, заключённый в круг, есть вписанный
Квадрат. В соответствии с вышеприведенной формулой его
Сторона равна:
Следовательно, квадрат со стороной 30 см невозможно выре зать
из круга диаметром 40 см.
ГЛАВА VII.
ОБ ОКРУЖНОСТИ.
165. Фигуры, вписанныя в круг и описанныe около него. Многоугольник, вершины котораго находятся на окружности, наз. вписанным в круг; на чер. 243-м представлены вписанные треугольник, четыреxугольник и пятиугольник.
Маогоугольник, которoго стороны касаются круга наз. описанным около круга; на чер. 244-м представлены описанные треуг. и четыреxуг.

166. Если требуется вписать в круг какой-нибудь нецравильный многоугольник, напр. семиугольник, то стоит только взягь на окружности 7 произвольных точек А, В, С... (чер. 245) и соедннить их прямыми линиями.
Если бы хотeли описать около круга четырехугольник, то слeдовало бы взять на окружности 4 точки и провести в этих точках касательные; от пересeчения касательных и образуется описан. четырехуг. (чер. 246).

167. Положим теперь, что нужно вписать в круг прав. многоуг., напр. пятиугольник. Для этого нужно раздeлить окружность на 5 равных частей; вся окружн.=360°, слeд. в пятой долe её будет 72°; поэтому построим при центрe круга (чер. 247) по транспортиру уг. 72° и будем хорду АВ откладывать по окружн.; она уложится ровно 5 раз-и тогда образуется 5-к.

Он будет правильный, потому что всe стороны его равны между собою; углы тоже равны, так как каждый из них измeряется половиною трех пятых окружности и слeд. содержит 108°.
Если бы нужно было вписать прав. 9-к, то слeдовало бы раздeлить окружность на 9 равных частей, т.е. построить при центрe уг. в 40°; при 20-кe надо построить уг. в 18°, и т. под.
Положим еще, что надо вписать прав. 7-к;
седьмая часть окружн.= 360 / 7 = 51 3 / 7 =51°25"42 6 / 7 ". На транспортирe не означены не только секупды, но и минуты; поэтому такого угла нельзя отложить точно-мы отложим непремeвно или больше, или меньше его; оттого и послeдняя сторона многоуг. выйдет или меньше или больше остальных сторон.
Гораздо точнeе вписывать прав.многоугольники без помощи транстортира, а посредством только циркуля и линейки; но таким способом можно вписывать только нeкоторые многоуг., напр. квад-рат, 6-к.
168. Чтоб вписать в круг квад-рат, должно раздeлить окружн. на 4 равныя части; а для этого надо (чер. 248) провести два перпевдикулярных диаметра;

если соединить концы их, то получим квадрат, потому что всe стороны его равны между собою, как хорды, стягивающие равные дуги; всe углы прямые, как имeющие вершину на окружности и опирающиеся на концы диаметра.
169. Чтоб вписать в круг прав. шестиугольн., отложим от какой-нибудь точки окружн. (чер. 249) хорду АВ = радиусу; тогда, проведя радиусы АО и ВО, получим равносторонний тр-к АОВ; слeд. уг. АВО=60°, и дуга АВ будет шестая часть окружн.; а потому хорда АВ отложится по окружн. ровно 6 раз.

170. Умeя вписывать прав. 6-к, легко уже вписать и прав. тр-к. Для этого должно раздeлить сперва окружность на 6 равных частей (чер. 250) в точках В, А, С, потом соединить точки А, С и Е; получим правильный тр-к АСЕ, потому что стороны его равны, так как каждой из них соотвeтствует дуга, составляющая 1 / 3 окружности.
171. Слeдующим саособом можно с достаточной точностью вписывать в круг всякий прав. многоуг. Чтобы вписать напр. нрав. 9-к, проводим в кругe (чер. 251) диам. АВ;

строим на АВ равностор. тр-к АВС; дeлим АВ на 9 равных частей; соединяем вершину С тр-ка со второй точкой дeления D и продолжаем прямую СD до пересeчения с окружн. в Е; хорда AЕ отложится по окружности 9 раз.
Если бы нужно было вписать прав. 5-к, то надо бы раздeлкгь диаметр на 5 равных частей (чер. 252); для 7-ка на 7 частей (чер. 253), и т. под.

172. Еcли какой-нибудь прав. многоуг. вписан в круг, то можно удвоить число сторон мн-ка, т.-е. вписать такой прав. мног., который имeл бы вдвое больше сторон.

Пусть напр. АВСDEG (чер. 254) будет прав. 6-к; опустим из центра О перпендикуляры на всe стороны мн-ка; тогда дуги AВ, ВС... раздeлятся пополам; соединив точки дeления с вершинами 6-ка, получим прав. 12-к. Опустив перпенд. на стороны этого 12-ка, впишем прав. 24-к, потом 48-к, и т. д.
Таким образом посредством циркуля и линейки мы можем вписывать в круг правильные 6-ки, 12-ки, 24-ки..., а также квадраты, 8-ки, 16-ки...
173. С увеличением числа сторон вписан. многоуг., самые стороны будут становиться все мельче и мельче, и периметр мн-ка будет болeе и болeе подходить к окруж., так что окружность можно считать за периметр такого прав. мн-ка, который имeет чрезвычайно много сторон.
174. Если в круг вписать прав. многоуг., то легко и описать прав. многоуг. того же числа сторон.

Пусть напр. AВСDЕ (чер. 255) будет прав. 5-к; опустим из центра на стороны мн-ка перпендикуляры и через точки M, N.. проведем касательные; тогда получится прав. описанный 5-к.
Можно также (чер. 256) провести касательные через вершины вписанного многоугольника.
175. Рассмотрим, около каких фигур можно описать круг. Мы уже знаем (§ 143), что через три точки, не лежащие на одной прямой линии, всегда можно провести окружность; слeд. около всякого треугольника можно описать круг .

Возьмем теперь четырехуг. АВСD (чер. 257). Проведем окружн. через три точки А, В, С (мы уже умeем это сдeлать); окружн. эта может пройти также и через точку D, но может и не пройти. Eсли она пройдет через D, то уг. D будет содержать столько градусов, сколько их содержится в 1 / 2 дуги АВС; а так как уг. B измeряется 1 / 2 дуги АDС, дуги же АВС и АDС составляют вмeстe цeлую окружн., то углы D и В составят в суммe 180°; но сумма всeх угл. четыреуг.=360°, cлeд. и А+С==180°.
Итак, круг можно описать только около такого четырехугольника, в котором сумма противолежащих углов=180°. Таким образом, можно описать круг около прямоуголь-ника, а около косоугольного параллелограмма нельзя.
176. Около всякого прав. многоуг. можно описать круг . Пусть АВСDЕF (чер. 258) есть прав. многоуг.; внутри его можно найти такую точку, которая будет находиться в равном расстоянии от всeх его вершин.

Чтобы сдeлать это, раздeлим углы А и В пополам линиями АО и ВО; точка пересeчения этих линий и будет искомая. Докажем, что линии АО, ВО, СО, DO...равны между собою.
Треуг. АВО = ОВС, потому что у них сторона ВО общая, АВ=ВС, как стороны прав. мн-ка, уг. т = уг. п , как половины угла В; сдeд. и линия АО = СО; но АО=ВО, потому что тр-к АВО равнобедр., так как уг. т =уг. р , как половины равных углов; слeд., всe три линии АО, ВО, СО равны между собою. Сравнивая тр-ки ВОС и СОD, найдем, что ВО= СО=ОD...; слeд. если из O радиусом ОА, или ВО, или OC... описать окружн., то она пройдет через вершины всeх углов многоугольника.
177. Eсли около прав. мн-ка (чер. 259) описан круг то стороны АВ, ВС... этого мн-ка будут в кругe хордами;

но равныe хорды находятся в равных раcстояниях от центра; слeд. перпендикуляры ОМ, ОN.., опущенные из центра O на стороны мн-ка, будут равны между собою, и если из O радиу-сом ОМ или ОN.. опишем круг, то он коснется всeх сторон мн-ка в точках М, N... Такой круг назыв. вписанным , а радиус его наз. апофемою мног-ка.
Итак, во всякой прав. многоуг. можно вписать круг .
Таким образом, центром кругов, описанного около мн-ка и вписанного, будет точка пересeчения линий, дeлящих два угла мн-ка пополам; радиусом описан. круга будет линия, соединяющая центр с вершиной одного из углов мн-ка; а радиусом вписан. круга или апофемою - перпендикуляр, опущенный из центра на одну из сто-рон мн-ка. Центр вписанного и описанного кругов наз. также центром правильного мн-ка.
178. Вопросы. 1) Какие мн-ки наз. вписанными в круг? описанными? 2) Вписать в круг какой-нибудь мн-к? описать? 3) Как вписать в круг посредством транспортира какой-нибудь прав. мн-к? 4) Как вписать в круг посредством циркуля и линейки квадрат? прав. 6-к? 5) Если прав. мн-к вписан в круг, то как вписать прав. мн-к, имeющий вдвое больше сторон? 6) Если прав. мн-к вписан в круг, то как описать прав. мн-к того же числа сторон? 7) Что дeлается с периметром прав. вписан. мн-ка при увеличении числа сторон его? 8) Всегда ли можно описать круг около тр-ка? 9) Доказать, что около всякого прав. мн-ка можно описать и вписать в него круг? 10) Можно ли вписать в круг параллелограмм? трапецию? 11) Что дeлается с периметром прав. описан. мн-ка при увеличении числа сторон его?
179. Задачи. 1) Вписать в круг 4-к? 8-к? 10-к? 15-к?
2) Описать около круга 4-к? 7-к? 3-к? 5-к?
3) Вписать в круг посредством трансп. прав. 10-в? 15-к? 20-к?
4) Вписать в круг посредством циркуля и линейки прав. 8-к?
5) Описать около круга посредством трансп. прав. 5-к? 9-к? 10-к?
6) Описать около круга посредством циркуля и линейки прав. 3-к? 6-к? квадрат? 12-к?
7) Около тр-ка описан круг, и центр его находится внутри тр-ка; какого вида этот тр-к? Какого вида был бы тр-к, если бы центр был на сторонe тр-ка? внe тр-ка?
8) Начертить посредством транспортира такой прав. 5-к, 8-к, 10-к, чтобы радиус описанного около него круга = линии т ?
9) Начертить посредством транспортира такой прав. 5-к, чтоб его апофема равнялась данной линии?
10) На данной прямой линии построить с помощью транспортира правильный 5-к? 8-к? 10-к?
11) В кругe проведена хорда; из концов её восставлены перпендикуляры до встрeчи с окружностью; точки встрeчи соединены прямою; какого вида получился четыреугольник?
12) Рад. круга=3,6 дюйм.; чему равен периметр описанного квадр.?
13) Доказать, что сторона вписанного в круг правильного тр-ка находится в расстоянии половины радиуса от центра этого круга?
14) В круг вписан 4-к; вершины его дeлят окружность на части, находящиеся в отношении 4:7:5:11; опредeлить углы 4-ка?
15) В круг вписан прав. тр-к, и сторона его отстоит на 7 1 / 2 дюйм. от центра этого круга; опредeлить радиус круга?
16) Доказать, что внутренний угол всякого прав. мн-ка служит дополнением до 180° тому углу, который получится от соединения двух сосeдних вершин этого мн-ка с его центром?
17) Доказать, что если хорда АВ (чер. 260) = радиусу круга О, а АО есть сторона прав. впис. 10-ка, то, соединив точку В с С, получим сторону прав. впис. 15-ка.

На данной прямой линии а построить помощью циркуля и линейки: 18) прав. тр-к? 19) квадрат? 20) прав. 6-к? 21) прав. 8-к? 22) прав. 12-к?
Посредством циркуля и линейки построить: 23) квадрат по рад. r опиcаннoго круга? 24) квадрат по апофемe а ? 25) прав. 6-к по рад. r опис. круга? 26) прав. 6-к по апофемe а ? 27) прав. 3-к по рад. r опис. круга? 28) прав. 3-к по апофемe а ?
29) В данный ромб вписать круг?
30) Описать круг около прямоугольника?
31) В кругe вписан тр-к; одна сторона его есть диаметр, а двe другие стягивают дуги, которых отношение есть 15: 17; опредeлить углы тр-ка?
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
«Урок теорема Пифагора» - Теорема Пифагора. Определить вид четырехугольника KMNP. Разминка. Знакомства с теоремой. Определить вид треугольника: План урока: Исторический экскурс. Решение простейших задач. И обрете лестницу долготою 125стоп. Вычислите высоту CF трапеции ABCD. Доказательство. Показ картинок. Доказательство теоремы.
«Объём призмы» - Понятие призмы. Прямая призма. Объем исходной призмы равен произведению S · h. Как найти объем прямой призмы? Призму можно разбить на прямые треугольные призмы с высотой h. Проведение высоты треугольника ABC. Решение задачи. Цели урока. Основные шаги при доказательстве теоремы прямой призмы? Изучение теоремы об объеме призмы.
«Многогранники призма» - Дайте определение многогранника. DABC – тетраэдр, выпуклый многогранник. Применение призм. Где применяются призмы? ABCDMP – октаэдр, составлен из восьми треугольников. ABCDA1B1C1D1 – параллелепипед, выпуклый многогранник. Выпуклый многогранник. Понятие многогранника. Многогранник А1А2..АnB1B2..Bn- призма.
«Призма 10 класс» - Призмой называется многогранник у которого грани находятся в параллельных плоскостях. Применение призмы в быту. Sбок.= Pоснован. + h Для прямой призмы: Sп.п = Pоснов. h + 2Sоснов. Наклонная. Правильная. Прямая. Призма. Формулы нахождения площади. Применение призмы в архитектуре. Sп.п = Sбок.+2Sоснован.
«Доказательство теоремы Пифагора» - Геометрическое доказательство. Значение теоремы Пифагора. Теорема Пифагора. Доказательство Евклида. «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Доказательства теоремы. Значение теоремы состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии.










